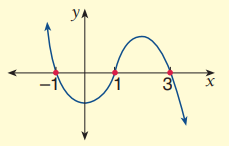
To find cubic equation from the given zeroes, x-intercepts, solutions or values of x, we use the formula given below.
y = k(x - a) (x - b) (x - c)
Here a, b and c are x-intercepts.
Difference between touches and crosses :

Here the curve crosses the x-axis at three different points.
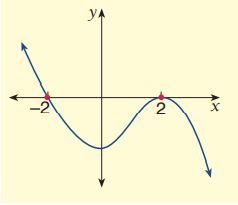
The curve crosses x-axis at -2 and touches the x-axis at 2. So, we have to take the factor (x - 2) twice. So, the equation would be y = (x + 2)(x - 2) 2
Find the equation of the cubic with graph :
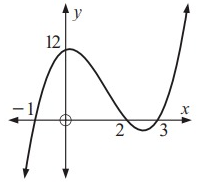
By observing the figure.
Given the points -1, 2 and 3
x = -1, x = 2 and x = 3
P(x) = a (x + 1) (x - 2) (x - 3) --- (1)
Since, the graph passes through the points are (0, 12).
The points (0, 12) substitute the equation (1).
12 = a (0 + 1) (0 - 2) (0 - 3)
Dividing 6 on each sides.
a = 2 substitute the equation (1).
P(x) = 2 (x + 1) (x - 2) (x - 3)
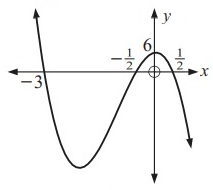
By observing the figure.
Given the points -3, -1/2 and 1/2
x = -3, x = -1/2 and x = 1/2
P(x) = a (x + 3) (x + 1/2) (x - 1/2)
= a (x + 3) 1/2[(2x + 1) (2x - 1)]--- (1)
Since, the graph passes through the points are (0, 6).
The points (0, 6) substitute the equation (1).
6 = a (0 + 3) 1/2[(2(0) + 1) (2(0) - 1)
a = -4 substitute the equation (1).
P(x) = -4 (x + 3) 1/2[(2x + 1) (2x - 1)]
= -2 (x + 3) (2x + 1) (2x - 1)
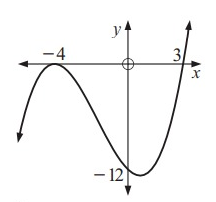
By observing the figure, the curve passes through 3 and touches at -4
P(x) = a (x + 4) 2 (x - 3) --- (1)
Since, the graph touches the points are (0, -12).
The points (0, -12) substitute the equation (1).
-12 = a (0 + 4) 2 (0 - 3)
Dividing -48 on each sides.
a = 1/4 substitute the equation (1).
P(x) = 1/4 (x + 4) 2 (x - 3)
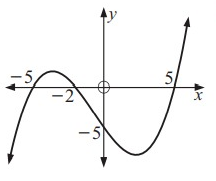
By observing the figure.
Given the points -5, -2 and 5
x = -5, x = -2 and x = 5
P(x) = a (x + 5) (x + 2) (x - 5) --- (1)
Since, the graph passes through the points are (0, -5).
The points (0, -5) substitute the equation (1).
-5 = a (0 + 5) (0 + 2) (0 - 5)
Dividing -50 on each sides.
a = 1/10 substitute the equation (1).
P(x) = 1/10 (x + 5) (x + 2) (x - 5)
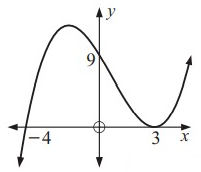
By observing the figure, the curve crosses the x-axis at -4 and touches 3. So, we repeat the factor (x - 3) twice.
P(x) = a (x + 4) (x - 3) 2 --- (1)
Since, the graph touches the points are (0, 9).
The points (0, 9) substitute the equation (1).
9 = a (0 + 4) (0 - 3) 2
Dividing 36 on each sides.
a = 1/4 substitute the equation (1).
P(x) = 1/4 (x + 4) (x - 3) 2
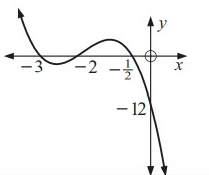
By observing the figure.
x = -3, x = -2 and x = -1/2
P(x) = a (x + 3) (x + 2) (x + 1/2)
= a (x + 3) (x + 2) 1/2(2x + 1)--- (1)
Since, the graph passes through the points are (0, -12).
The points (0, -12) substitute the equation (1).
-12 = a (0 + 3) (0 + 2) 1/2(2(0) + 1)
a = -4 substitute the equation (1)
P(x) = -4 (x + 3) (x + 2) 1/2(2x + 1)
= -2 (x + 3) (x + 2 ) (2x + 1)